SAT-solver
Demo: tarvk.github.io/SAT
The satisfiability problem is the problem of checking whether a given proposition (boolean formula) is satisfiable. A proposition is built-up of boolean variables, negations, conjunctions, disjunctions, implications, and bi-implications.
a && b => c describes the boolean formula stating that if a and b are both true, c must also be true. This formula will be true or false depending on the assignments of a, b, and c. For this formula it's true for all assignments of a, b and c except for when a and b are true, and c is false.
Some formulas however may be true for none of the assignments of its variables. Such a formula is called a contradiction. Other formulas may be true for all of the assignments of its variables. Such a formula is called a tautology. Finally all other formulas are called contingencies.
A formula is satisfiable if there exists an assignment of variables to make it true. Thus this is the opposite of being a contradiction. This satisfiability problem is NP-hard, meaning that it's believed no algorithm exists that can efficiently solve this problem for every input formula. This however does not mean that no algorithm exists that can efficiently solve this problem for some formulas, but it's always possible to find a formula for which such an algorithm is in efficient. Here "inefficient" means that it has an exponential runtime, so adding even a single variable to the input could double how long the computation takes.
In the "Automated reasoning" course which I took at university we used existing SAT-solvers (which solve satisfiability problems) to solve arbitrary problems which we encoded into boolean formulas. The course also covered the high-level functioning of such solvers and discussed three algorithms that can be used for SAT-solving. I made my website in order to play around with this theory, as well as to be able to compare the performance of these different techniques.
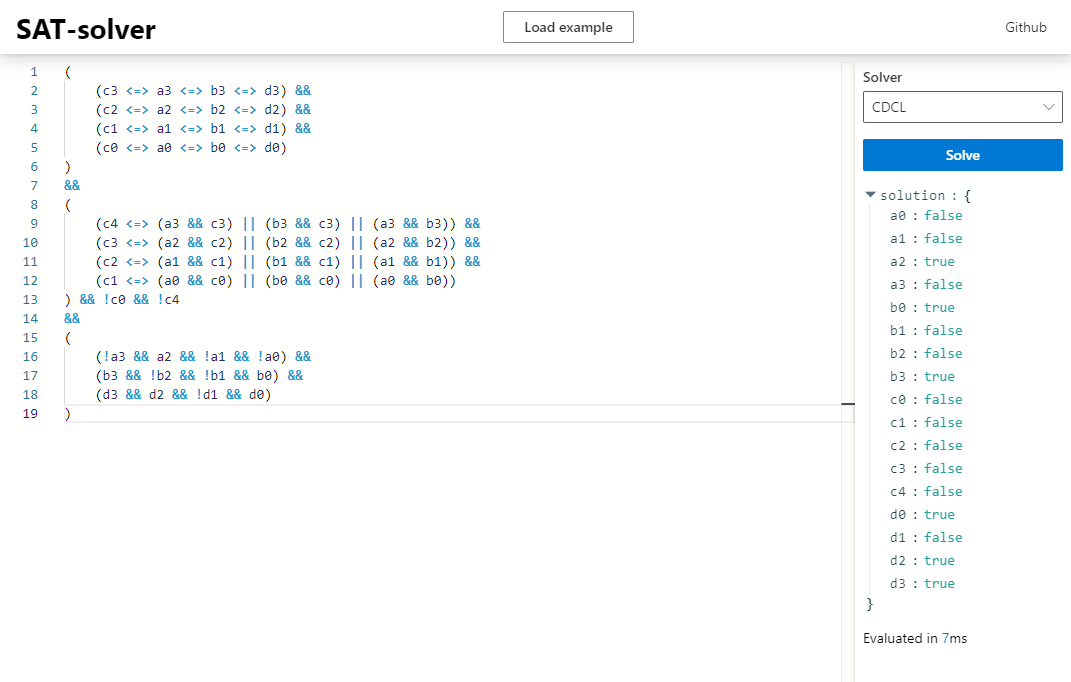
Here you can see how my website can be used to find a satisfying assignment for a rather big formula in only a couple of milliseconds:
Aspects
Parser
In this project I played around with parsers, and fell in love with Parsimmon.
For the web-editor I had to convert the text input into a hierarchical formula to operate on, so I had to parse this input. I've manually made recursive descent parsers in the past and also used different libraries before, but Parsimmon was by far the best experience. Parsimmon initially looked very confusing to me, but once I understood the basic concept, it was a breeze to work with. The main power of Parsimmon is how flexible it is due to its composable approach. You simply create small parsers and combine them together to make bigger parsers.
Using Parsimmon I built my own higher-level wrapper that simplify parsing of algebra syntaxes such as propositional logic.
Every operator is able to specify its own functionality as well as parsing type. You can find these operators in the formula/constructs directory.
These operators and their parser definitions can then be combined into a complete language with its corresponding parser as can be seen in formula/defaultLanguage.ts.
I'm really happy with how clean this structure turned out, and how easy it is to add new operators using this system. I'm planning on using similar setups in other future projects.
Satisfiability checker
In this project I first implemented the Tseytin transformation which is able to translate any formula into a CNF formula which is satisfiable if and only if the original formula is satisfiable.
After the formula is in CNF, there are 3 algorithms that can operate on it:
The first two are not very interesting, and were very trivial to implement. They also are not very efficient, but DPLL can still be used for some simple formulas.
Conflict Driven Clause Learning (CDCL) was very interesting to implement however. I had to look up some additional information in order to manage this, since my first attempt failed. After carefully going through cse442-17f.github.io/CDCL and users.aalto.fi/CDCL I eventually managed to get my implementation working, and I think my final code is actually quite neat. This code can be viewed at solver/procedures/CDCL.
Website
The website itself was added on top of the project, simply to serve as a demo. I used a stack that's quite common for me:
In this website I also used the Monaco Editor which is a really great web-based code editor. It allowed me to even create a custom syntax for my propositional logic, such that text is nicely highlighted.
I also added 2 examples to the webpage that were discussed in the course. These examples can be used to generate propositional formulas from, so you can see how the different algorithms handle larger inputs.